手性声子是一种特殊的晶格激发,其实空间图像对应原子的圆极化运动(如图1)。这种声子模式可存在于不具备镜面(2D)以及中心对称性(3D)的系统中。当该声子模式对应的电声耦合强度足以使得该模式发生软化后,便会导致一种螺旋式的晶格畸变以及电荷密度分布,即手性电荷密度波态。该团队计算了单层TiSe2的声子谱,发现了其中非手性声子的软化,会诱导形成非手性电荷密度波态,而手性声子的软化则会导致手性电荷密度波的形成,这在数值计算上验证了该理论的正确性(如图2所示)。结合这项理论,该团队提出非线性电/磁致伸缩效应(nonlinear electro-/magnetostrictive effect)可作为调控手性电荷密度波的有效途径。此外,当前探测手性电荷密度波的实验方法仍有待拓展。通常,手性电荷密度波可以利用镜面对称的动量点上衍射峰的强度不同来表征。然而衍射峰的强度区别往往取决与很多因素,并且这种区别亦可能不甚明显。该团队在考虑了多声子的热散射效应后,计算了更符合实际情况的X射线衍射。他们发现,对于手性电荷密度波态,X射线衍射斑点的各向异性也破缺了镜面对称性(图3),相较于非手性结构呈现出明显的偏转。这证明了衍射峰的各项异性亦可作为探测手性电荷密度波的实验手段。该研究给出了一种手性电荷密度波相变的机制、探测和调控方法、以及新的实验观测手段,为关于手性电荷密度波以及相关物性的研究奠定了坚实的基础。该文近期发表于npj Computational Materials 10, 264 (2024)。
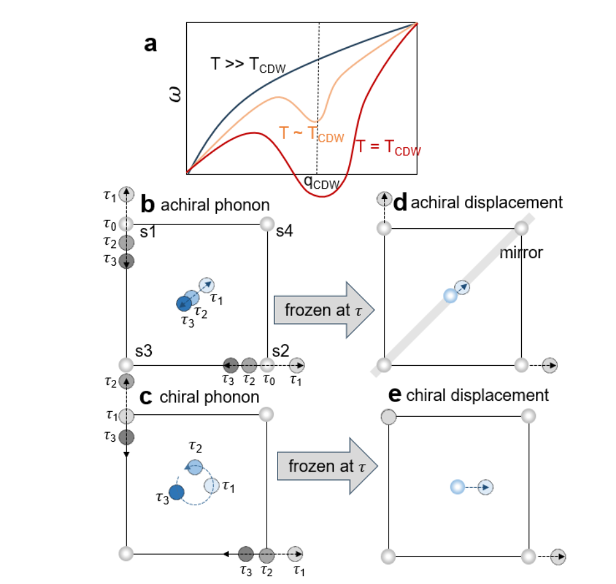
图1 (a)声子在温度降低当临界点( )时声子发生软化;(b)若该声子不是手性声子,其振动模式不会破坏镜面,以及中心对称性,对应于非手性CDW态(d);(c)若该声子是手性声子,其振动模式破坏了镜面,以及中心对称性,对应于手性CDW态(e)。
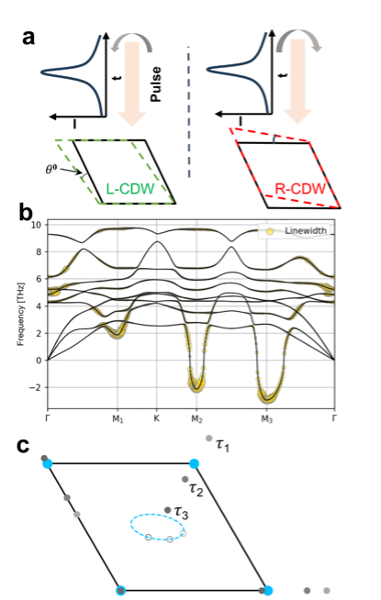
图2 通过外场调控(a),使得由镜面对称性联系的声子模式的软化程度不同(b),进而诱导出软化的手性声子。对应于破缺了镜面对称性的声子模式(c)。
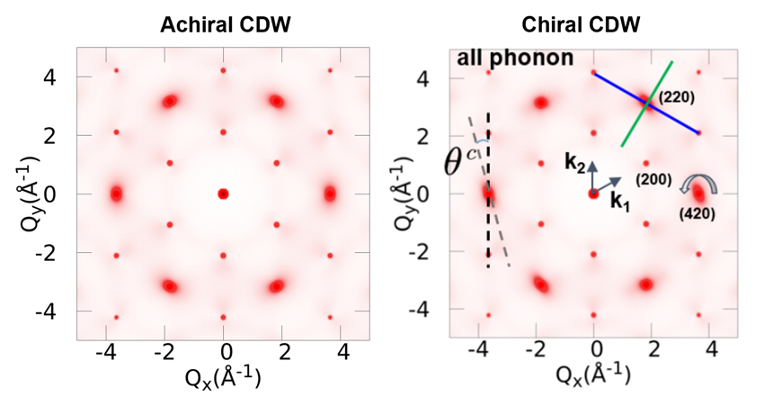
图3 考虑了多声子散射效应后,计算得到的XRD衍射图谱。非手性声子对应的XRD峰的各向异性保持了镜面对称性(左图),而手性声子对应的XRD峰的各向异性破坏了镜面对称性,呈现出明显的偏转角(右图)。









